
The scaled maximum step length allowed in line search. The maximum allowed number of iterations. Set this keyword to force the computation to be done in double-precision arithmetic. If the routine does converge to a local minimum, try restarting from a different initial guess to obtain the global minimum. Use the CHECK keyword to specify a named variable which will be set to 1 if the routine has converged to a local minimum or to 0 if it has not. NEWTON calls an internal function named fmin() to determine whether the routine has converged to a local minimum rather than to a global minimum (see Numerical Recipes, section 9.7). We write a function NEWTFUNC to express these relationships in the IDL language: FUNCTION newtfunc, X RETURN, + X - 3.0, X^ 2 + X^ 2 - 9.0] END Keywords This function must accept an n-element vector argument X and return an n-element vector result.įor example, suppose the non-linear system is defined by the following equations: VecfuncĪ scalar string specifying the name of a user-supplied IDL function that defines the system of non-linear equations. Note: If NEWTON is complex then only the real part is used for the computation. ArgumentsĪn n-element vector containing an initial guess at the solution of the system. The result is an n-element vector containing the solution. Result = NEWTON( X, Vecfunc ) Return Value Provide an initial guess as the algorithm's starting point: Systems of non-linear equations may have multiple solutions starting the algorithms with different initial guesses enables detection of different solutions.
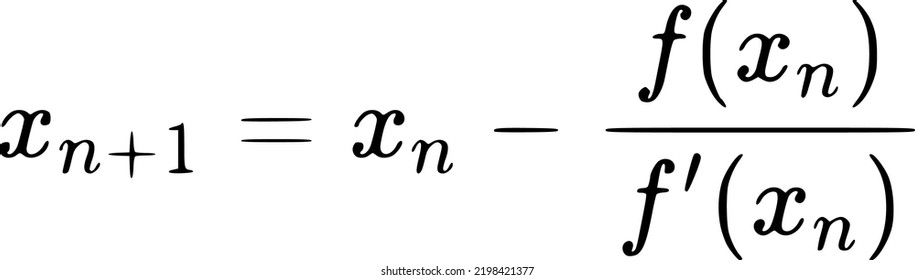
Use NEWTON to solve an n-dimensional system of n non-linear equations. NEWTON is based on the routine newt described in section 9.7 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission. The NEWTON function solves a system of n non-linear equations in n dimensions using a globally-convergent Newton’s method.


 0 kommentar(er)
0 kommentar(er)
